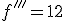CALCULO DIFERENCIAL

EJERCICIOS

Pendiente de la recta tangente

La pendiente de la recta tangente a una curva en un punto es la derivada de la función en dicho punto.

Recta tangente a una curva en un punto

ejemplo

Hallar la ecuación de la recta tangente a la parábola y = x² − 5x + 6 paralela a la recta 3x + y − 2 = 0.

y = −3x + 2

La pendiente de la recta es el coefeciente de la x. m = −3

Dos rectas paralelas tienen la misma pendiente.

f'(a) = 2a − 5

2a − 5 = −3a = 1

P(1, 2)

y − 2 = −3 (x − 1)y = −3x + 5

Obsevamos que como la recta es paralela a la dada tiene la misma

Teorema de Rolle

En calculo diferencial, el teorema de Rolle demuestra la existencia de un punto interior en un intervalo abierto para el cual la derivada de una función derivable se anula cuando el valor de ésta en los extremos del intervalo es el mismo. Es generalizado mediante el teorema del valor medio, del que este es un caso especial. Es uno de los principales teoremas en cálculo debido a sus aplicaciones.

Si f es una funcion en la que cumple (i) f es una funcion (ii) f es diferenciable en el intervalo abierto (a,b)

(iii) f (a) =0 y f(b) = 0

Teorema de valor medio

En cálculo diferencial, el teorema de valor medio (de Lagrange), teorema de los incrementos finitos, teorema de Bonnet-Lagrange o teoría del punto medio es una propiedad de las funciones derivables en un intervalo. Algunos matemáticos consideran que este teorema es el más importante del cálculo (ver también el teorema fundamental del cálculo integral). El teorema no se usa para resolver problemas matemáticos; más bien, se usa normalmente para demostrar otros teoremas. El teorema de valor medio puede usarse para demostrar el teorema de Taylor ya que es un caso especial.

Criterio de la segunda derivada

El Criterio o prueba de la segunda derivada es un teorema o método del cálculo matemático en el que se utiliza la segunda derivada para efectuar una prueba simple correspondiente a los máximos y mínimos relativos.

Se basa en el hecho de que si la gráfica de una función f es convexa en un intervalo abierto que contiene a f´(c)=0,f(c), y debe ser un mínimo relativo de . De manera similar, si la gráfica de una función es cóncava hacia abajo en un intervalo abierto que contiene a f´(c)=0,f(c) y debe ser un máximo relativo de f.

Sea f una función tal que f´(x)=0 y la segunda derivada de existe en un intervalo f abierto que contiene a x.

1. Si f´´(x)>0 , entonces tiene un máximo relativo en .

2. Si f´´(x)<0 , entonces tiene un mínimo relativo en .

1. Si f´(x)=0 , entonces el criterio falla. Esto es,f quizás tenga un máximo relativo en (x,f(x)), un mínimo relativo en o ninguno de los dos. Tomar como ejemplo la función f(x) = x³. En tales casos, se puede utilizar el criterio de la primera derivada o el criterio de la tercera derivada.

Análisis de la variación de funciones

Cuando la variación total de cualquier función particular es finita, en ese caso, esa función se conoce como Función de Variación Acotada, que puede ser abreviada como función BV (Bounded Variation por sus siglas en inglés). El gráfico correspondiente de la función BV se dice entonces que se comporta bien en un sentido preciso. La función BV tiene amplias aplicaciones en el campo de las matemáticas, y es utilizada en algunos de los teoremas más importantes, tal como son los Teoremas de Fourier. En el caso de la funciones continuas que contienen sólo una variable, la variación acotada implica la distancia finita cubierta por un punto a lo largo del eje y. Otra clasificación establece que las funciones de variación acotada, tienen la propiedad de intervalo cerrado, son las funciones que se pueden establecer como la diferencia entre dos monótonas acotadas.

La variación Acotada de una función determinada en el intervalo [x, y] puede ser establecida como

Donde S es el conjunto acotado:

La variación resulta ser infinita si el conjunto no es acotado. El supremo de S puede ser llamado también como Variación Total o sólo la variación de f y se denota como V (f; x, y) o simplemente V (x). Existen ciertos teoremas que pueden ser útiles para el análisis de la variación de la función:

1). Si en el conjunto [x, y], la función está incrementando, en ese caso, es la función de variación acotada en el conjunto [x, y] y consecuentemente V [g [x, y]] = g(y) – g(x).

2). Si en el conjunto [x, y] la función es constante, entonces es la función de variación acotada en el conjunto [x, y] y entonces V [g [x, y]] = 0.

3) En el conjunto [x, y] si, g y f son las funciones de variación acotada y c es constante, en ese caso

a). g es una función de variación acotada en el intervalo [x, y].

b). g es una función de variación acotada en cada subintervalo cerrado del intervalo [x, y].

c). cg es también una función BV en el conjunto [x, y].

d). g + f y g –f son BV en el conjunto [x, y]

e). gf es también BV en el conjunto [x, y].

Algunos datos más útiles acerca de estas funciones especiales se pueden establecer como que una función de variación acotada se puede expresar también por la divergencia de 2 funciones crecientes.

Derivadas de orden superior

Sea f(x) una función diferenciable, entonces se dice que f '(x) es la primera derivada de f(x). Puede resultar f '(x) ser una función derivable, entonces podriamos encontrar su segunda derivada, es decir f(x). Mientras las derivadas cumplan ser funciones continuas y que sean derivables podemos encontrar la n-ésima derivada. A estas derivadas se les conoce como derivadas de orden superior.

Ejemplo

Regla l ́hôpital

En matemáticas más específicamente en el calculo diferencial la regla de l'Hôpital o regla de l'Hôpital-Bernoulli¹ es una regla que usa derivadas para ayudar a evaluar limite de funciones que estén en forma indeterminada.

Sean f y g dos funciones continuas definidas en el intervalo [a,b], derivables en (a,b) y sea c perteneciente a (a,b) tal que f(c)=g(c)=0 y g'(x)≠0 si x≠c.

Si existe el límite L de f'/g' en c, entonces existe el límite de f/g (en c) y es igual a L. Por lo tanto.

Derivaciones implicitas

Funciones implícitas

Una correspondencia o una función está definida en forma implícita cuando no aparece despejada la y sino que la relación entre x e y viene dada por una ecuación de dos incógnitas cuyo segundo miembro es cero.

Derivadas de funciones implícitas

Para hallar la derivada en forma implícita no es necesario despejar y. Basta derivar miembro a miembro, utilizando las reglas vistas hasta ahora y teniendo presente que:

x'=1.

En general y'≠1.

Por lo que omitiremos x' y dejaremos y'.

CALCULO DIFERENCIAL UNIDAD 4 Y 5

Derivada

En matemática, la derivada de una función es una medida de la rapidez con la que cambia el valor de dicha función matemática, según cambie el valor de su variable independiente. La derivada de una función es un concepto local, es decir, se calcula como el límite de la rapidez de cambio media de la función en un cierto intervalo, cuando el intervalo considerado para la variable independiente se torna cada vez más pequeño. Por ello se habla del valor de la derivada de una cierta función en un punto dado.

Un ejemplo habitual aparece al estudiar el movimiento: si una función representa la posición de un objeto con respecto al tiempo, su derivada es la velocidad de dicho objeto. Un avión que realice un vuelo transatlántico de 4500 km entre las 12:00 y las 18:00, viaja a una velocidad media de 750 km/h. Sin embargo, puede estar viajando a velocidades mayores o menores en distintos tramos de la ruta. En particular, si entre las 15:00 y las 15:30 recorre 400 km, su velocidad media en ese tramo es de 800 km/h. Para conocer su velocidad instantánea a las 15:20, por ejemplo, es necesario calcular la velocidad media en intervalos de tiempo cada vez menores alrededor de esta hora: entre las 15:15 y las 15:25, entre las 15:19 y las 15:21, etc.

Entonces el valor de la derivada de una función en un punto puede interpretarse geométricamente, ya que se corresponde con la pendiente de la recta tangente a la gráfica de la función en dicho punto. La recta tangente es a su vez la gráfica de la mejor aproximación lineal de la función alrededor de dicho punto. La noción de derivada puede generalizarse para el caso de funciones de más de una variable con la derivada parcial y el diferencial.

La derivada de una función f en un punto x se denota como f′(x). La función cuyo valor en cada punto x es esta derivada es la llamada función derivada de f, denotada por f′. El proceso de encontrar la derivada de una función se denomina diferenciación, y es una de las herramientas principales en el área de las matemáticas conocida como cálculo infinitesimal. Concretamente, el que trata de asuntos vinculados con la derivada se denomina cálculo diferencial.

Conceptos de incremento y de razón de cambio. La derivada de una función.

Derivada de una función en un punto. Dada la función f(x) continúa en el intervalo abierto I, se define la derivada en el punto “a” como:

Sí en lugar de considerar h el incremento de la variable independiente x lo sustituimos por Δx tenemos que la definición queda:

En el caso de que hagamos h=x-a tenemos a+h=x, y la definición nos queda de la siguiente forma:

Función derivada. Dada la función f(x) continúa en el intervalo abierto I denominamos función derivada a:

Sí en lugar de considerar h el incremento de la variable independiente x lo sustituimos por Δx tenemos que la definición queda:

La interpretación geométrica de la derivada.

La derivada de una función en un punto representa el valor de la pendiente de la recta tangente en dicho punto. La pendiente está dada por la tangente del ángulo que forma la recta tangente a la curva (función) con el eje de las abcisas, en ese punto.

La derivada de una función mide el coeficiente de variación de dicha función. Es decir, provee una formulación matemática de la noción del coeficiente de cambio. El coeficiente de cambio indica lo rápido que crece (o decrece) una función en un punto (razón de cambio promedio) respecto del eje $x\,$ de un plano cartesiano de dos dimensiones. Por ejemplo si tomamos la velocidad de algo, su coeficiente es la aceleración, la cual mide cuánto cambia la velocidad en un tiempo dado.