lunes, 5 de octubre de 2015

LIMITE, CONTINUIDAD Y DISCONTINUIDAD

Límite

En matemática, el concepto de límite es una noción topológica que formaliza la noción intuitiva de aproximación hacia un punto concreto de una sucesión o una función, a medida que los parámetros de esa sucesión o función se acercan a determinado valor.

En cálculo infinitesimal (especialmente en análisis real y matemático) este concepto se utiliza para definir los conceptos fundamentales de convergencia, continuidad, derivación,integración, entre otros. Si bien, el concepto de límite parece intuitivamente relacionado con el concepto de distancia, en un espacio euclídeo, es la clase de conjuntos abiertosinducidos por dicha métrica, lo que permite definir rigurosamente la noción de límite.

El concepto se puede generalizar a otros espacios topológicos, como pueden ser las redes topológicas; de la misma manera, es definido y utilizado en otras ramas de la matemática, como puede ser la teoría de categorías.

Para fórmulas, el límite se utiliza usualmente de forma abreviada mediante lim como en lim(a_n) = a o se representa mediante la flecha (→) como en a_n → a.

Si f(x) es una función usual (polinómicas, racionales, radicales, exponenciales, logarítmicas, etc.) y está definida en el punto a, entonces se suele cumplir que:

Es decir: para calcular el límite se sustituye en la función el valor al que tienden las x.

No podemos calcular límite

porque el dominio de definición está en el intervalo [0, ∞), por tanto no puede tomar valores que se acerquen a −2.

Sin embargo sí podemos calcular límite

, porque aunque 3 no pertenezca al dominio, D=

− {2, 3}, sí podemos tomar valores del dominio tan próximos a 3 como queramos.

CONTINUIDAD

En matemáticas, una función continua es aquella para la cual, intuitivamente, para puntos cercanos del dominio se producen pequeñas variaciones en los valores de la función. Si la función no es continua, se dice que es discontinua. Una función continua de

\R

\R

es aquella cuya gráfica puede dibujarse sin levantar el lápiz del papel (más formalmente su grafo es un conjunto conexo).

La continuidad de funciones es uno de los conceptos principales del análisis matemático y de la topología. El artículo describe principalmente la continuidad de funciones realesde una variable real.

Intuitivamente, la continuidad significa que un pequeño cambio en la variable x implica sólo un pequeño cambio en el valor de f(x), es decir, la gráfica consiste de un sólo trozo de curva.

En contraste, una gráfica como la de la función f(x) = sgn x (signo de x) que consiste de pedazos de curva separados por un vacío en una abcisa exhibe allí una discontinuidad.

La continuidad de la función f(x) para un valor a significa que f(x) difiere arbitrariamente poco del valor f(a) cuando x está suficientemente cerca de a.

Expresemos esto en términos del concepto de límite.

DISCONTINUIDAD

Una discontinuidad en matemática es un punto de una función y=f(x) en la cual la misma sufre un "salto" o cambio "brusco" de valor. Se verifica una discontinuidad cuando el valor de la función en un punto difiere del límite de esa función cuando nos acercamos a ese punto por derecha y por izquierda.

Continuidad por la izquierda

Una función f(x) es continua por la izquierda en el punto a si existe f(a) y lim_x->a-f(x) = f(a).

Continuidad por la derecha

Una función f(x) es continua por la derecha en el punto a si existe f(a) y lim_x->a+f(x) = f(a).

La función anterior es continua por la izquierda en x=2, pero no por la derecha.

Tipos de discontinuidades

\left \{ \begin{array}{l} Discontinua { \color{Red} \left \{ \begin{array}{l} Evitable \\ No \; evitable { \color{PineGreen} \left \{ \begin{array}{l} De \; primera \; especie { \color{Blue} \left \{ \begin{array}{l} De \; salto \; finito \\ De \; salto \; infinito \\ Asint \acute{o} tica \end{array} \right . }\\ \\ De \; segunda \; especie \end{array} \right . } \\ \end{array} \right . } \\ Continua \end{array} \right .

Discontinuidad evitable

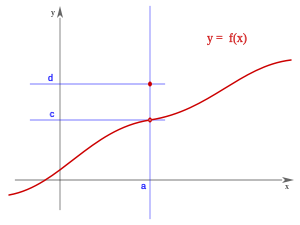
Una función presenta discontinuidad evitable en un punto a, si tiene límite en un punto, pero la función en ese punto tiene un valor distinto o no existe, veamos estos dos casos.

Si el límite cuando x tiende a a, es c, y el valor de la función evaluada en a es d, la función es discontinua en a.

\left \{ \begin{array}{l} \left . \begin{array}{l} \underset{x \to {a}^{-}}{\text{lím}} \; f(x) = c \\ \\ \underset{x \to {a}^{+}}{\text{lím}} \; f(x) = c \end{array} \right \} \underset{x \to {a}}{\text{lím}} \; f(x) = c \\ \\ f(a) = d \end{array} \right .

Discontinuidad de primera especie

En este tipo de discontinuidad existen tres tipos:

De salto finito

Existen el límite por la derecha y por la izquierda del punto, su valor es finito, pero no son iguales:

A este tipo de discontinuidad de primera especie se le llama salto finito, y el salto viene dado por:

Salto = \Big| \lim_{x\to {a}^{-}}f(x)-\lim_{x\to {a}^{+}}f(x) \Big|

Si la función tiende a c, cuando x tiende a a por la izquierda, y tiende a d cuando lo hace por la derecha, en el punto x = a, se presenta un salto, independientemente del valor de la función en ese punto.

\left \{ \begin{array}{l} \underset{x \to {a}^{-}}{L \acute{\imath}m} \; f(x) = c \\ \\ \underset{x \to {a}^{+}}{L \acute{\imath}m} \; f(x) = d \\ \\ \nexists f(a) \end{array} \right .

De salto infinito

Si uno de los límites laterales es infinito y el otro finito, tanto si el límite por la izquierda es finito y el de la derecha infinito:

\left . \begin{array}{c} \underset{x \to {a}^{-}}{L \acute{\imath}m} \; f(x) = L \\ \\ \underset{x \to {a}^{+}}{L \acute{\imath}m} \; f(x) = \pm \infty \end{array} \right \} \quad Discontinuidad \; de \; salto \; infinito

Así podemos ver los casos:

\left \{ \begin{array}{l} \underset{x \to {a}^{-}}{L \acute{\imath}m} \; f(x) = c \\ \\ \underset{x \to {a}^{+}}{L \acute{\imath}m} \; f(x) = + \infty \end{array} \right .

Discontinuidad asintótica

Si los dos límites laterales de la función en el punto x= a son infinitos:

\left . \begin{array}{c} \underset{x \to {a}^{-}}{L \acute{\imath}m} \; f(x) = \pm \infty \\ \\ \underset{x \to {a}^{+}}{L \acute{\imath}m} \; f(x) = \pm \infty \end{array} \right \} \quad Discontinuidad \; asint \acute{o} tica

A este tipo de discontinuidad de primera especie se le llama discontinuidad asintótica, siendo x= a la asíntota.

\left \{ \begin{array}{l} \underset{x \to {a}^{-}}{L \acute{\imath}m} \; f(x) = + \infty \\ \\ \underset{x \to {a}^{+}}{L \acute{\imath}m} \; f(x) = + \infty \end{array} \right .

Discontinuidad de segunda especie[editar]

Si la función no existe en uno de los lados del punto, o no existen alguno, o ambos, de los límites laterales de la función en ese punto, se dice que la función presenta una discontinuidad de segunda especie en ese punto.

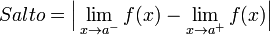
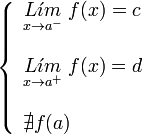
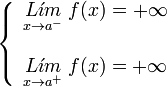
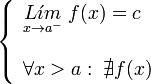
\left \{ \begin{array}{l} \underset{x \to {a}^{-}}{L \acute{\imath}m} \; f(x) = c \\ \\ \forall x > a: \; \nexists f(x) \end{array} \right .

FUNCIONES TRIGONOMETRICAS

Las funciones trigonométricas se definen comúnmente como el cociente entre dos lados de un triángulo rectánguloasociado a sus ángulos. Las funciones trigonométricas son funciones cuyos valores son extensiones del concepto de razón trigonométrica en un triángulo rectángulo trazado en una circunferencia unitaria (de radio unidad). Definiciones más modernas las describen como series infinitas o como la solución de ciertas ecuaciones diferenciales, permitiendo su extensión a valores positivos y negativos, e incluso a números complejos.

Existen seis funciones trigonométricas básicas. Las últimas cuatro, se definen en relación de las dos primeras funciones, aunque se pueden definir geométricamente o por medio de sus relaciones. Algunas funciones fueron comunes antiguamente, y aparecen en las primeras tablas, pero no se utilizan actualmente ; por ejemplo el verseno (1 − cos θ) y la exsecante (sec θ − 1).

Función	Abreviatura	Equivalencias (en radianes)
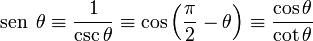
Seno	sen, sin	$\sen \; \theta \equiv \frac{1}{\csc \theta} \equiv \cos \left(\frac{\pi}{2} - \theta \right) \equiv \frac{\cos \theta}{\cot \theta} \,$
Coseno	cos	$\cos \theta \equiv \frac{1}{\sec \theta} \equiv \sen \left(\frac{\pi}{2} - \theta \right) \equiv \frac{\sen \theta}{\tan \theta} \,$
Tangente	tan, tg	$\tan \theta \equiv \frac{1}{\cot \theta} \equiv \cot \left(\frac{\pi}{2} - \theta \right) \equiv \frac{\sen \theta}{\cos \theta} \,$
Cotangente	ctg (cot)	$\cot \theta \equiv \frac{1}{\tan \theta} \equiv \tan \left(\frac{\pi}{2} - \theta \right) \equiv \frac{\cos \theta}{\sen \theta} \,$
Secante	sec	$\sec \theta \equiv \frac{1}{\cos \theta} \equiv \csc \left(\frac{\pi}{2} - \theta \right) \equiv \frac{\tan \theta}{\sen \theta} \,$
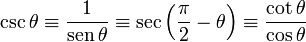
Cosecante	csc (cosec)	$\csc \theta \equiv \frac{1}{\sen \theta} \equiv \sec \left(\frac{\pi}{2} - \theta \right) \equiv \frac{\cot \theta}{\cos \theta} \,$

Definiciones respecto de un triángulo rectángulo

Para definir las razones trigonométricas del ángulo:

\alpha

, del vértice A, se parte de un triángulo rectángulo arbitrario que contiene a este ángulo. El nombre de los lados de este triángulo rectángulo que se usará en los sucesivo será:

La hipotenusa (h) es el lado opuesto al ángulo recto, o lado de mayor longitud del triángulo rectángulo.
El cateto opuesto (a) es el lado opuesto al ángulo $\alpha$ .
El cateto adyacente (b) es el lado adyacente al ángulo $\alpha$ .

Todos los triángulos considerados se encuentran en el Plano Euclidiano, por lo que la suma de sus ángulos internos es igual a π radianes (o 180°). En consecuencia, en cualquier triángulo rectángulo los ángulos no rectos se encuentran entre 0 y π/2 radianes. Las definiciones que se dan a continuación definen estrictamente las funciones trigonométricas para ángulos dentro de ese rango:

1) El seno de un ángulo es la relación entre la longitud del cateto opuesto y la longitud de la hipotenusa:

$\sen \alpha = \frac {{ \color{ForestGreen}\textrm{opuesto}}} {{ \color{Red}\textrm{hipotenusa}}} = \frac {a} {h}$

El valor de esta relación no depende del tamaño del triángulo rectángulo que elijamos, siempre que tenga el mismo ángulo

\alpha

, en cuyo caso se trata de triángulos semejantes.

2) El coseno de un ángulo es la relación entre la longitud del cateto adyacente y la longitud de la hipotenusa:

$\cos \alpha = \frac {{ \color{Blue}\textrm{adyacente}}} {{ \color{Red}\textrm{hipotenusa}}} = \frac {b} {h}$

3) La tangente de un ángulo es la relación entre la longitud del cateto opuesto y la del adyacente:

$\tan \alpha = \frac {{ \color{ForestGreen}\textrm{opuesto}}} {{ \color{Blue}\textrm{adyacente}}} = \frac {a} {b}$

4) La cotangente de un ángulo es la relación entre la longitud del cateto adyacente y la del opuesto:

$\cot \alpha = \frac {{ \color{Blue}\textrm{adyacente}}} {{ \color{ForestGreen}\textrm{opuesto}}} = \frac {b} {a}$

5) La secante de un ángulo es la relación entre la longitud de la hipotenusa y la longitud del cateto adyacente:

$\sec \alpha = \frac {{ \color{Red}\textrm{hipotenusa}}} {{ \color{Blue}\textrm{adyacente}}} = \frac {h} {b}$

6) La cosecante de un ángulo es la relación entre la longitud de la hipotenusa y la longitud del cateto opuesto:

$\csc \alpha = \frac {{ \color{Red}\textrm{hipotenusa}}} {{ \color{ForestGreen}\textrm{opuesto}}} = \frac {h} {a}$

Radián

El radián es la unidad de ángulo plano en el Sistema Internacional de Unidades. Representa el ángulo central en una circunferencia y abarca un arco cuya longitud es igual a la del radio. Su símbolo es rad. Hasta 1995 tuvo la categoría de unidad suplementaria en el Sistema Internacional de Unidades, junto con el estereorradián. A partir de ese año, y hasta el momento presente, ambas unidades figuran en la categoría de unidades derivadas.

Esta unidad se utiliza primordialmente en física, cálculo infinitesimal, trigonometría, goniometría, etc.

En general, si tenemos una circunferencia de radio r, y un cierto ángulo a subtendiendo un arco de longitud s, el cociente s/r nos da el valor de ese ángulo en radianes.

Por otra parte, nosotros conocemos que la mitad de la circunferencia corresponde a un arco de longitud pr, mitad que equivale a un ángulo de 180° , lo cual nos permite hacer transformaciones entre radianes y ángulos:

Por ejemplo, ¿ cuántos radianes son 30° ?.

Respuesta: considerando la relación

tenemos que x = p/6 radianes.

Otro ejemplo, ¿ cuántos grados son 0,357 radianes ?.

Respuesta: considerando la relación

tenemos que x = 20,45° .

* Es interesante también recordar que 1 radián son 180°/p , es decir, 57,29... grados. Mientras que 1 grado son p/180° , o sea, 0,1745... radianes.

* PROPIEDADES INMEDIATAS

* Según esta definición de radian, puede establecerse la siguiente relación entre un ángulo a y el arco de circunferencia subtendido:

s = a . r

es decir, la longitud del arco s es el producto del ángulo a (en radianes) por el radio del circulo.

* Algunas equivalencias entre ángulos en grados y en radianes:

Grádos	Radian.
30°	p/6
60°	p/3
90°	p/2
120°	2p/3
180°	p
270°	3p/2
360°	2p

NOTA: Es muy práctico conocer "de memoria" la tabla presente, pues con ello ganamos en "velocidad de cálculo". Algunos ejemplos:

Ejemplo 1: Queremos conocer rápidamente a qué equivalen 75° , entonces:

75° = 60° + 15° -> p/3 + (1/2) p/6 -> 5p/12

Ejemplo 2: Queremos conocer rápidamente a qué equivalen 265° , entonces:

265° = 270° - 5° -> 3p/2 - (1/6) p/6 -> 53p/36

* La circunferencia trigonométrica.

Se trata de una circunferencia imaginaria de radio r = 1, lo cual conduce a que la relación s = a . r, se reduzca a:

s = a

Esta circunferencia además facilita que podamos trazar fácilmente sobre ella los valores del seno, coseno y tangente de un determinado ángulo en radianes:

Si tenemos un ángulo a en una circunferencia trigonométrica como la de la figura, la longitud del cateto vertical (marcado en rojo) será el valor de sin a, puesto que la hipotenusa vale 1. Análogamente, la longitud del cateto horizontal (marcado en azul) es el valor de cos a.

En el presente ejemplo tanto el seno como el coseno son positivos, pues se encuentran o bien arriba del eje horizontal, o bien a la derecha del vertical. Pero pueden darse otros casos:

El ángulo de la figura 1 se halla en el cuadrante II y tiene como seno un valor positivo (en azul), el coseno (en rojo) tiene un valor negativo. En la figura 2, el ángulo se halla en el cuadrante III y ambos valores son negativos.

Nosotros podemos trazar este tipo de circunferencias trigonométricas para hacer diversas consideraciones sobre senos y cosenos de ciertos ángulos.

Por ejemplo:

En la figura 1 tenemos dos ángulos que se diferencia en p/2, sean a, b, con el mayor siendo b = a + p/2, entonces como puede apreciarse en la circunferencia trigonométrica los dos triángulos que aparecen sobre ella son iguales, pero lo que es el seno para el ángulo pequeño es el coseno (con signo negativo) para el grande, y lo que es el coseno para el pequeño es es seno para el grande. Por tanto podemos escribir:

sin (a + p/2) = cos a cos (a + p/2) = - sin a

En la figura 2 tenemos dos ángulos cuya suma es p (llamados ángulos suplementarios), sean a, b, con el mayor siendo b = p - a, entonces se puede apreciar que ambos senos coinciden, mientras que los cosenos tienen la misma longitud pero signos opuestos. Es decir:

sin (p - a ) = sin a cos ( p - a ) = - cos a

El alumno deberá acostumbrarse a manejar estas relaciones entre senos y cosenos de ángulos ayudándose de la circunferencia trigonométrica.

* Un caso especial: la tangente.

También podemos utilizar la circunferencia trigonométrica para hacer evaluaciones de tangentes de ángulos, aunque en este caso puede ser suficiente la consideración de que la tangente es el cociente de seno entre coseno.

Tangente de un ángulo que se halle en el cuadrante I..

Si nos fijamos en la circunferencia de arriba, para el ángulo a tenemos que su tangente es la longitud del segmento marcado en verde, puesto que sabemos que: tga = a/b, es decir, seno entre coseno, por lo tanto según el teorema de Tales aplicado a los triángulos semejantes:

ahora bien, la tangente es la línea verde de la figura de arriba que al estar sobre el eje horizontal es positiva, como efectivamente tiene que ser pues a/b es una cantidad positiva en el cuadrante I. Pero hay que tener cuidado con lo que sucede en los cuadrantes II y III. Veamos:

La tangente de un ángulo que se halle en el cuadrante II debe considerarse negativa.

Para estos casos la línea verde nos da el valor de la tangente (sin el signo), sin embargo hay que considerar que el sentido de la tangente puede diferir del de a/b. En el ejemplo de arriba, para un ángulo en el cuadrante II, la línea verde nos da el valor de la tangente sin embargo ésta es negativa, como así lo indica a/b. Una anomalía similar nos ocurre con los ángulos del cuadrante III, cuya línea de la tangente la tenemos que trazar hacia abajo y sin embargo esa tangente es positiva. En el cuadrante IV no hay esa anomalía.